Задача:
Пусть P={p1,p2,…,pn} является перестановкой чисел 1,2,…,n. Таблицей инверсий перестановки P называют последовательность T={t1,t2,…,tn},в которой ti равно числу элементов перестановки P,стоящих в P левее i и больших i. Написать программу,которая по заданной таблице инверсий восстанавливает перестановку.
Решение
О инверсиях
Пусть a1 a2 … an — перестановка множества {1,2,…,n}. Если i<j и ai > aj, то пара (ai,aj) называется инверсией перестановки; например, перестановка 3 1 4 2 имеет три инверсии: (3,1), (3,2) и (4,2). Каждая инверсия — это пара элементов, «нарушающих порядок»; следовательно, единственная перестановка, не содержащая инверсий, — это рассортированная перестановка 1 2 … n.
Понятие инверсии ввел Г. Крамер в 1750 году в связи со своим замечательным правилом решения линейных уравнений.
Таблица инверсии b1 b2 … b3 перестановки a1 a2 … an образуется, если определить bj как число элементов слева от j, которые больше, чем j. Другими словами, bj — число инверсий, второй элемент которых равен j. Отсюда, например, следует, что таблицей инверсии перестановки
будет
поскольку 5 и 9 расположены левее 1; 5,9,8 — левее 2 и т.д. Всего эта перестановка имеет 20 инверсий. По определению числа bj всегда удовлетворяют неравенствам
Пожалуй, наиболее важный факт, касающийся перестановок и установленный Маршаллом Холлом(Marshall Hall), состоим в том, что таблица инверсий единственным образом определяет соответствующую перестановку. Из любой таблицы инверсии b1 b2 … bn, удовлетворяющей условиям (*), можно однозначно восстановить перестановку, которая ее породила, путем последовательного определения относительного расположения элементов n, n -1,…,1 (в этом порядке).
Примеры инверсий
Пример 1
Восстановить перестановку по таблице инверсий
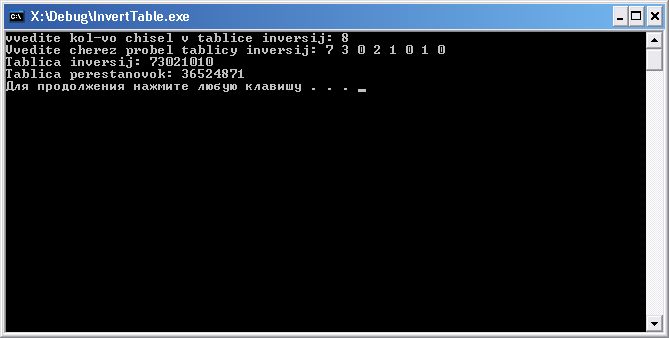
таблица исходная [1,2,3,4,5,6,7,8]
таблица инверсии [7,3,0,2,1,0,1,0]
Решение
Перестановка содержит 8 номеров. Восстановление начинаем с числа 8. Ставим это число на неопределенное пока место
В позиции 7 в таблице инверсий стоит число 1, следовательно, 7 стоит правее 8.
В позиции 6 в таблице инверсий стоит 0, следовательно, 6 стоит левее всех уже поставленных чисел
В позиции 5 в таблице инверсий стоит число 1, следовательно, 5 стоит правее 6.
В позиции 4 в таблице инверсий стоит 2, следовательно, 4 стоит правее двух поставленных чисел, считая слева
В позиции 3 в таблице инверсий стоит 0, следовательно, 3 стоит левее всех уже поставленных чисел
В позиции 2 в таблице инверсий стоит 3, следовательно, 2 стоит правее трех поставленных чисел, считая слева
И, наконец, в первой позиции стоит 7. Ставим 1 на последнем месте, так, что перед 1 будет 7 чисел, больших 1.
Получаем искомую перестановку
Результат:
таблица исходная [1,2,3,4,5,6,7,8]
таблица инверсии [7,3,0,2,1,0,1,0]
Таблица перест. [3,6,5,2,4,8,7,1]
Восстановление перестановки по таблице инверсий
Пример 2
Восстановить перестановку по таблице инверсий
таблица исходная [1,2,3,4,5,6,7,8,9]
таблица инверсии [5,0,1,3,8,4,2,6,8]
Решение
Перестановка содержит 9 номеров. Восстановление начинаем с числа 9. Ставим это число на неопределенное пока место
В позиции 8 в таблице инверсий стоит число 6, следовательно, 8 стоит правее 9.
В позиции 7 в таблице инверсий стоит 2, следовательно, 7 стоит правее на 2 числа всех уже поставленных чисел, считая слева.
В позиции 6 в таблице инверсий стоит число 4, следовательно, 6 стоит правее на 4 числа всех уже поставленных чисел, считая слева.
В позиции 5 в таблице инверсий стоит 8, следовательно, 5 стоит правее на 8 числа всех уже поставленных чисел, считая слева.
В позиции 4 в таблице инверсий стоит 3, следовательно, 4 стоит правее на 3 числа всех уже поставленных чисел, считая слева.
В позиции 3 в таблице инверсий стоит 1, следовательно, 3 стоит правее на 1 число всех уже поставленных чисел, считая слева.
В позиции 2 в таблице инверсий стоит 0, следовательно, 2 стоит поставить слева от поставленных чисел.
И, наконец, в первой позиции стоит 5, следовательно, 1 стоит правее на 5 чисел всех уже поставленных чисел, считая слева.
Получаем искомую перестановку
Результат:
таблица исходная [1,2,3,4,5,6,7,8,9]
таблица инверсии [5,0,1,3,8,4,2,6,8]
Таблица перест. [2,9,3,8,7,1,4,6,5]
Алгоритм
Входной параметр таблица инверсии. Начинаем цикл от конца таблицы инверсии до начала, на каждом шаге проверяем 2 условия:
если в таблице инверсии текущий элемент равен 0, то в таблицу перестановок пишем номер элемента с самого начала;
если в таблице инверсии текущий элемент равен k и , то на k позиций смещаем относительно начала таблицы перестановок.
В конце получаем таблицу перестановок.
Программирование
В качестве структуры, которая будет хранить таблицу перестановок, используется строка (string).
функции, которые нам понадобятся:
- конкатенация (объединение строк)
- length() (длина строки)
- insert(pos,str) (вставить в позицию pos строку str)
По ходу цикла проверяем 3 условия:
если число в таблице инверсии = 0, то объединяем номер элемента в таблице инверсии с сторокой перестановок;
если число в таблице инверсии равно k и k меньше длины строки, то вставляем в строку перестановок в позицию k номер элемента;
если число в таблице инверсии равно k и k больше длины строки, то объединяем строку перестановок с номером элемента.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | #include "stdafx.h" #include <string> // библиотека классов для работы с типом строка #include <iostream> using namespace std; // работы с консолью ввода и вывода int _tmain(int argc, _TCHAR* argv[]) { cout << "vvedite kol-vo chisel v tablice inversij: " ; // вывода на экран int kol = 0; // переменная для учета количества элементов в массиве cin >> kol; // ввод с клавиатуры количества чисел в матрице инверсий cout << "Vvedite cherez probel tablicy inversij: "; // вывод на экран int *mas_in; // создание указателя для динамического массива mas_in = new int(kol); // создание динамического массива размера kol for (int i=0;i<kol;i++) // цикл для ввода элементов динамического массива cin >> mas_in[i]; // ввод с клавиатуры i элемента cout << "Tablica inversij: "; // вывод на экран for (int i=0;i<kol;i++) //цикл для вывода динамического массива инверсий cout << mas_in[i]; // вывод i элемента cout << endl; // вывод с новой строки string strP = ""; // строка выходная char chislo[2]; // для преобразования из числа в строку for (int i=0;i<kol;i++) // цикл перебора всех элементов матрицы инверсий // для последовательности 1 ... 9 , начинаем с 9 if (mas_in[kol-i-1] == 0) // если элемент матрицы инверсий равен 0, то сдвигаем влево strP = itoa(kol-i,chislo,10) + strP; // переводим в строку номер порядковый kol-i и прибавляем всю остальную строку else // если элемент матрицы инверсий не нулевой, то на n позиций надо передвинуть число в право от начала строки if (strP.length() > mas_in[kol-i-1]) // если длина выходной строки больше, то мы может вставить внутрь строки число strP.insert(mas_in[kol-i-1],itoa(kol-i,chislo,10)); //вставляем в строку на mas_in[kol-i-1] вправо else strP += itoa(kol-i,chislo,10); // иначе просто прибавляем к концу строки cout << "Tablica perestanovok: " << strP << endl; // выводим нашу строку, в которой подряд идет последовательность перестановок system("PAUSE"); // пауза для нажатия Enter return 0; } |
Скриншоты
Ссылки для скачивания
Литература
- Доналяд Э Кнут,Ю. В Козаченко,В. Т Тертышная,И. В Красиков «Искусство программирования: Сортировка и поиск», том 3.